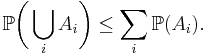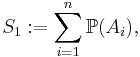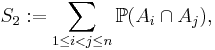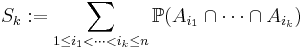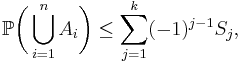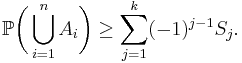Boole's inequality

In probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events. Boole's inequality is named after George Boole.

Formally, for a countable set of events A1, A2, A3, ..., we have

{\mathbb P}\biggl(\bigcup_{i} A_i\biggr) \le \sum_i {\mathbb P}(A_i).

In measure-theoretic terms, Boole's inequality follows from the fact that a measure (and certainly any probability measure) is σ-sub-additive.

Bonferroni inequalities

Boole's inequality may be generalised to find upper and lower bounds on the probability of finite unions of events. These bounds are known as Bonferroni inequalities, after Carlo Emilio Bonferroni, see Bonferroni (1936).

Define

S_1�:= \sum_{i=1}^n {\mathbb P}(A_i),

and

S_2�:= \sum_{1\le i<j\le n} {\mathbb P}(A_i \cap A_j),

as well as

S_k�:= \sum_{1\le i_1<\cdots<i_k\le n} {\mathbb P}(A_{i_1}\cap \cdots \cap A_{i_k} )

for all integers k in {3, ..., n}.

Then, for odd k in {1, ..., n},

{\mathbb P}\biggl( \bigcup_{i=1}^n A_i \biggr) \le \sum_{j=1}^k (-1)^{j-1} S_j,

and for even k in {2, ..., n},

{\mathbb P}\biggl( \bigcup_{i=1}^n A_i \biggr) \ge \sum_{j=1}^k (-1)^{j-1} S_j.

Boole's inequality is recovered by setting k = 1. When k = n, then equality holds and the resulting identity is the inclusion–exclusion principle.

See also

References

This article incorporates material from Bonferroni inequalities on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.